قضیه هال (۱۹۳۵) قضیهای مربوط به شاخه ترکیبیات و قضیهٔ گراف در ریاضی است. این قضیه که به ریاضیدان انگلیسی، فیلیپ هال نسبت داده میشود، شرط لازم و کافی برای وجود تطابق کامل در گرافهای دوبخشی را بیان میکند. گرافهای دوبخشی به گرافهایی گفته میشوند که رأسها به دو دسته مجزا قابل افراز هستند بگونهای که تمامی یالهای گراف بین گرههای بین دو دسته مختلف باشند.
تعاریف
۱-مسیر M-متناوب: مسیری است که یالهای آن یکی در میان در تطابق M باشد.
۲-مسیر M-افزوده: مسیر M-متناوبی است که یالهای ابتدایی و انتهایی آن داخل تطابق M نباشد.
در تطابق بیشینه مسیر M-افزوده وجود ندارد زیرا اگر فرض کنیم که یک مسیر M-افزوده در تطابق بیشینه ما وجود داشته باشد میتوان با حذف یالهایی از مسیر افزوده که در تطابق هستند از تطابق و اضافه کردن یالهایی که در تطابق نیستند به تطابق اندازه تطابق را یک یال افزایش داد که این متناقض با بیشینه بودن تطابق است.
قضیه ی ازدواج هال و نظریهٔ گراف
کمک گفتن از قضیهٔ گراف برای اثبات قضیهٔ هال به کمک گرافهای دو بخشی،که اثبات میشود شرایط کافی و لازم برای وجود حداقل یک تطابق برای یک سمت گراف وجود دارد.
(G(X+Y,E را یک گراف دو بخشی محدود با دو بخش X و Y در نظر بگیرید برای یک مجموعه از رئوس از مجموعه X مجموعه N را تعریف میکنیم که به هسایگیهایی از w در G(مجموعهای از ئوس از Y که در همسایگی با بعضی از عنصرهای w هستند براساس قضیهٔ ازدواج هال یک تطابق وجود دارد که کل x را پوشش دهد اگر و تنها اگر برای هر زیر مجموعه w از X رابطه روبرو برقرار باشد: |N|>= |w| یعنی هر زیر مجموعه w از X به اندازه کافی راس همسایه در Y دارد. برای یگ گراف دو بخشی (G(X+Y,E که با دو بخشX و Y با اندازه یکسان تئوری هال یک شرایط کافی و لازم برای وجود یک تطابق کامل در گراف است. یک راه حل برای گراف اصلی که الزاماً دو بخشی نیست توسط قضیهٔ Tutte ارائه میشود.
اثبات قضیه هال به کمک قضیه ی گراف
ابتدا اثبات می کنیم که اگ گراف دو بخشی (G(X+Y,E دارای یک تطابق کامل برای X است آنگاه |N|>= |w| برای همه wهایی که زیر مجموعه X هستند. فرض کنید M یک تطابق است که هر درجه از X را در بر میگیرد همه رئوس Y را که توسط M برای یک w مطابق شدهاند به صورت (M(w نشان می دهیم بنابراین
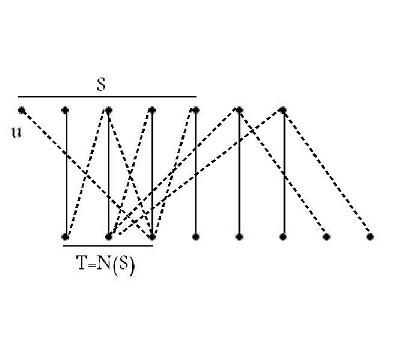
حال اثبات می کنیم اگر برای همه wهای زیر مجموعه X آنگاه (G(X+Y,E یک تطابق که هر راس را در X پوشش میدهد. شرایطی را فرض کنید که (G(X+Y,E یک گراف دو بخشی است که هیچ تطابقی برای آن که همه رأسهای X را پوشش دهد وجود نداردM را یک تطابق ماکسیمم در نظر بگیرید و u را یک راس که توسطM پوشش داده نشدهاست در نظ بگیرید مسیرهای تناوبی را در نظر بگیرید(مسیرهایی از G که بهطور تناوبی از رأسهای بیرون و درون M استفاده میکند از u شروع می کنیم مجموعهٔ همه راسهایی از Y که به u متصل هستند در مسیر تناوبی را T می نامیم و همه راسهایی از X که به u متصل هسند توسط مسیر تناوبی را (که شامل خود u میشود) را w در نظر بگیرید.
ر راس در T را به وسیلهٔ M به راس مطابق شدهاست در مقابل هر راس v در Y که به راس w در W مطابق شدهاست T توسط M یک به یک و پوشانسبت به T است که نتیجه میدهد:
از طرف دیگر(N(W زیرمجموعه Tاست v را در Y که به راس w از W وصل است در نظر بگیرید اگر یال(W,N) در M وحود داشته باشد آنگاه v براساس قسمت قبلی اثبات در T قرار دارد در غیر اینصورت ما میتوانیم یک مسیر تناوبی که در w به پایان میرسد بیابیم و آن را به N گسترش دهیم بک مسیر افزایشی در نظر بگیرید و نشان دهید که v در T است از این رو |W| -1 =|T| = |N|
اثبات قضیه هال
لزوم شرط : اگر برای یک مجموعه S شرط فوق برقرار نباشد چون تعداد همسایهها کمتر است پس راسی وجود دارد که برای تطبیق راسی ندارد.
کفایت شرط : داریم به ازای هر زیرمجموعه S از X، تعداد همسایههای S از تعداد اعضای S ناکمتر است. اگرM مجموعه X را اشباع نکند یک مجموعه S را پیدا میکنیم که شرط را نقض کند. فرض کنید u یک راس اشباع نشده در تطابق M باشد. S و T به ترتیب مجموعه راسهایی در X و Y است که از u میتوان با مسیرهای M-متناوب به آنها رسید. ادعا میکنیم که M، مجموعه T را با S-u جور میکند. مسیرهای M-متناوب از u به وسیلهٔ یالهایی که در تطابق وجود ندارد به Y و به وسیلهٔ یالهایی که در M باشد به X میرسد. چون هیچ مسیر M-افزوده وجود ندارد، هر راس از T در M وجود دارد. علاوه بر این، هر راس از S به جز u از راه یالی در M از راسی در T در دسترس است. از این رو این یالهای M یک نگاشت دوسویی میان T و S-uبرقرار میکند و داریم : تطابق میان T و S-u مستلزم آن است که T زیر مجموعه همسایههای S باشد. در واقع، T برابر مجموعه همسایههای S است. یک یال میان S و یک راس y عضو Y-T میتوانست یالی باشد که در M نباشد؛ این میتوانست یک مسیر M-متناوب با y بسازد، که با اینکه y در T نباشد در تناقض است. با در نظر گرفتن اینکه T برابر مجموعه همسایههای S است درمیابیم که تعداد همسایههای S که همان T است برابر است که کمتر از S است. بنابراین مجموعه S با فرض قضیه در تناقض است.